Thông tin liên hệ
- 036.686.3943
- admin@nguoicodonvn2008.info

Đề bài: Cho n bậc cầu thang, một người đứng ở dưới chân cầu thang muốn leo lên đỉnh. Người này có thể bước 1 bậc hoặc 2 bậc mỗi lần. Đếm số cách người đó có thể làm để lên tới đỉnh.
Bạn có thể nhìn ví dụ trong ảnh. Giá trị của n là 3 và có 3 cách để bước lên đỉnh.
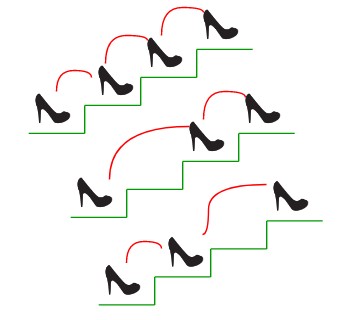
Ví dụ:
Input: n = 1
Output: 1
There is only one way to climb 1 stair
Input: n = 2
Output: 2
There are two ways: (1, 1) and (2)
Input: n = 4
Output: 5
(1, 1, 1, 1), (1, 1, 2), (2, 1, 1), (1, 2, 1), (2, 2)
Trong bài viết này, Quản Trị Mạng sẽ cùng các bạn tìm hiểu cách viết chương trình đếm số cách leo cầu thang bằng Bạn phải đăng nhập để xem liên kết .
Ta dễ dàng nhận thấy tính chất đệ quy trong bài toán này. Người đó có thể đến bậc thang thứ n từ bậc thang thứ n-1 hoặc bậc thang thứ n-2. Do đó, đối với mỗi bậc thang n, chúng ta hãy cố gắng tìm ra số cách để đi đến bậc thang thứ n-1 và n-2 và thêm chúng để đưa ra câu trả lời cho bậc thang thứ n. Với cách tiếp cận này, chúng ta có biểu thức sau:
ways(n) = ways(n-1) + ways(n-2)
Biểu thức trên thực chất là biểu thức của các số Fibonacci nhưng có một điều cần lưu ý là giá trị của ways(n) bằng với fibonacci(n+1).
ways(1) = fib(2) = 1
ways(2) = fib(3) = 2
ways(3) = fib(4) = 3
Để hiểu rõ hơn, chúng ta hãy tham khảo cây đệ quy bên dưới đây:
Input: N = 4
fib(5)
'3' / \ '2'
/ \
fib(4) fib(3)
'2' / \ '1' / \
/ \ / \
fib(3) fib(2)fib(2) fib(1)
/ \ '1' / \ '0'
'1' / '1'\ / \
/ \ fib(1) fib(0)
fib(2) fib(1)
Vì vậy, chúng ta có thể sử dụng hàm cho số Fibonacci để tìm giá trị của ways(n). Dưới đây là code mẫu:
# Python program to count
# ways to reach nth stair
# Recursive function to find
# Nth fibonacci number
def fib(n):
if n <= 1:
return n
return fib(n-1) + fib(n-2)
# Returns no. of ways to
# reach sth stair
def countWays(s):
return fib(s + 1)
# Driver program
s = 4
print "Số cách là = ",
print countWays(s)
# Contributed by Harshit Agrawal
Làm thế nào để đếm số cách nếu một người có thể leo m bậc cầu thang với một số m cho trước. Ví dụ m là 4 thì người đó có thể leo 1 bậc thang, 2 bậc thang, 3 bậc thang hoặc 4 bậc thang cùng lúc.
Để khái quát hóa cách tiếp cận trên, chúng ta có thể sử dụng quan hệ đệ quy sau:
ways(n, m) = ways(n-1, m) + ways(n-2, m) + ... ways(n-m, m)
Trong cách tiếp cận này, để đến cầu thang thứ n, hãy thử leo lên tất cả số bậc thang ít hơn n so với cầu thang hiện tại.
Sau đây là code mẫu cho phần khái quát này:
# A program to count the number of ways
# to reach n'th stair
# Recursive function used by countWays
def countWaysUtil(n, m):
if n <= 1:
return n
res = 0
i = 1
while i<= m and i<= n:
res = res + countWaysUtil(n-i, m)
i = i + 1
return res
# Returns number of ways to reach s'th stair
def countWays(s, m):
return countWaysUtil(s + 1, m)
# Driver program
s, m = 4, 2
print "Số cách là =", countWays(s, m)
# Contributed by Harshit Agrawal
Chúng ta cũng có thể sử dụng cách tiếp cận từ dưới lên của dp để giải quyết vấn đề này.
Chúng ta có thể tạo một mảng dp[] và khởi tạo nó với -1.
Bất cứ khi nào chúng ta thấy rằng một bài toán con không được giải quyết, chúng ta có thể gọi phương thức đệ quy.
Mặt khác, chúng ta dừng đệ quy nếu bài toán con đó đã được giải quyết.
Code mẫu như sau:
# Python program to count number of
# ways to reach Nth stair
# A simple recursive program to
# find N'th fibonacci number
def fib(n, dp):
if (n <= 1):
return 1
if(dp[n] != -1 ):
return dp[n]
dp[n] = fib(n - 1, dp) + fib(n - 2, dp)
return dp[n]
# Returns number of ways to
# reach s'th stair
def countWays(n):
dp = [-1 for i in range(n + 1)]
fib(n, dp)
return dp[n]
# Driver Code
n = 4
print("Số cách là = " + str(countWays(n)))
# This code is contributed by shinjanpatra
Cách này sử dụng kỹ thuật Dynamic Programming để giải quyết bài toán.
Chúng ta tạo ra một bảng res[] theo cách từ dưới lên bằng cách sử dụng mối quan hệ sau:
res[i] = res[i] + res[i-j] for every (i-j) >= 0
Do đó, chỉ số thứ i của mảng sẽ chứa số cách cần thiết để bước tới bậc thứ i có tính đến tất cả các khả năng leo (tức là từ 1 tới i).
Dưới đây là code mẫu theo cách tiếp cận này:
# A program to count the number of
# ways to reach n'th stair
# Recursive function used by countWays
def countWaysUtil(n, m):
# Creates list res with all elements 0
res = [0 for x in range(n)]
res[0], res[1] = 1, 1
for i in range(2, n):
j = 1
while j<= m and j<= i:
res[i] = res[i] + res[i-j]
j = j + 1
return res[n-1]
# Returns number of ways to reach s'th stair
def countWays(s, m):
return countWaysUtil(s + 1, m)
# Driver Program
s, m = 4, 2
print "Số cách là =", countWays(s, m)
# Contributed by Harshit Agrawal
Trong cách này, chúng ta sẽ sử dụng Dymanic Programming Approach một cách hiệu quả hơn.
Trong cách tiếp cận cho cầu thang thứ i này, chúng ta giữ một cửa sổ chứa tổng số m cầu thang cuối cùng mà có thể từ đó chúng ta leo lên cầu thang thứ i. Thay vì chạy một vòng lặp bên trong, chúng ta duy trì kết quả của vòng lặp bên trong một biến tạm thời. Chúng ta xóa các phần tử của cửa sổ trước đó và thêm phần tử của cửa sổ hiện tại.
Dưới đây là code mẫu:
# Python3 program to count the number
# of ways to reach n'th stair when
# user climb 1 .. m stairs at a time.
# Function to count number of ways
# to reach s'th stair
def countWays(n, m):
temp = 0
res = [1]
for i in range(1, n + 1):
s = i - m - 1
e = i - 1
if (s >= 0):
temp -= res[s]
temp += res[e]
res.append(temp)
return res[n]
# Driver Code
n = 5
m = 3
print('Số cách là =', countWays(n, m))
# This code is contributed by 31ajaydandge
Trong cách tiếp cận này, chúng ta chỉ đơn giản là đếm số số tập hợp có 2. Phương pháp này chỉ được áp dụng nếu như vấn đề thứ tự trong khi đếm bước không quan trọng.
# Here n/2 is done to count the number 2's in n
# 1 is added for case where there is no 2.
# eg: if n=4 ans will be 3.
# {1,1,1,1} set having no 2.
# {1,1,2} ans {2,2} (n/2) sets containing 2.
print("Number of ways when order "
"of steps does not matter is : ", 1 + (n // 2))
# This code is contributed by rohitsingh07052
Trong cách này, chúng ta sử dụng kỹ thuật Matrix Exponentitation để giải quyết bài toán.
Số lượng cách để bước lên bậc thang thứ n (có xét thứ tự) bằng với tổng lượt cách bước lên bật thang thứ n-1 và bậc thang thứ n-2.
Điều này tương ứng với mối quan hệ lặp lại sau:
f(n) = f(n-1) + f(n-2)
f(1) = 1
f(2) = 2
trong đó f(n) chỉ số cách bước tới bậc thang thứ n.
Lưu ý:
f(1) = 1 vì chỉ có 1 cách bước lên đỉnh cầu thang có 1 bậc, n=1, {1}
f(2) = 2 vì chỉ có 2 cách bước lên đỉnh cầu thang có 1 bậc, n=2, {1,1},{2}
Nó là một loại quan hệ truy hồi tuyến tính với các hệ số không đổi và chúng ta có thể giải chúng bằng phương pháp lũy thừa ma trận. Về cơ bản, phương pháp này tìm ma trận biến đổi cho một quan hệ truy hồi đã cho và áp dụng lặp lại phép biến đổi này cho một vectơ cơ sở để tìm ra giải pháp.
F(n) = CN-1F(1)
trong đó C là ma trận biến đổi, F(1) là vectơ cơ sở và F(n) là giải pháp mong muốn.
Do đó, trong trường hợp của chúng ta ma trận C sẽ là:
0 1
1 1
CN-1 có thể được tính toán bằng kỹ thuật Divide and Conquer, trong O((K^3) Log n) với K là kích thước của C.
Và F(1):
1
2
Ví dụ, cho n=4:
F(4) = C3F(1)
C3 =
1 2
2 3
Do vậy, C3F(1) =
5
8
Code mẫu như sau:
# Computes A*B
# where A,B are square matrices
def mul(A, B, MOD):
K = len(A);
C = [[0 for i in range(K)] for j in range(K)] ;
for i in range(1, K):
for j in range(1, K):
for k in range(1, K):
C[i][j] = (C[i][j] + A[i][k] * B[k][j]) % MOD;
return C;
# Computes A^n
def power( A, n):
if (n == 1):
return A;
if (n % 2 != 0):
# n is odd
# A^n = A * [ A^(n-1) ]
A = mul(A, power(A, n - 1), 1000000007);
else:
# n is even
# A^n = [ A^(n/2) ] * [ A^(n/2) ]
A = power(A, n // 2);
A = mul(A, A, 1000000007);
return A;
def ways(n):
F = [0 for i in range(3)];
F[1] = 1;
F[2] = 2;
K = 2;
MOD = 1000000007;
# create K*K matrix
C = [[0 for i in range(K+1)] for j in range(K+1)];
'''
* A matrix with (i+1)th element as 1 and last row contains constants [ [0 1 0 0
* ... 0] [0 0 1 0 ... 0] [0 0 0 1 ... 0] [. . . . ... .] [. . . . ... .] [c(k)
* c(k-1) c(k-2) ... c1] ]
'''
for i in range(1,K):
C[i][i + 1] = 1;
# Last row is the constants c(k) c(k-1) ... c1
# f(n) = 1*f(n-1) + 1*f(n-2)
C[K][1] = 1;
C[K][2] = 1;
if (n <= 2):
return F[n];
# f(n) = C^(n-1)*F
C = power(C, n - 1);
result = 0;
# result will be the first row of C^(n-1)*F
for i in range(1,K+1):
result = (result + C[1][i] * F[i]) % MOD;
return result;
# Driver code
if __name__ == '__main__':
n = 4;
print("Số cách là = " , ways(n) , "");
# This code is contributed by gauravrajput1
Cho một mảng A{a1, a2, ..., am} chứa tất cả các bước hợp lệ, tính số bước cần thiết để bước lên bậc thang thứ n, có tính thứ tự.
Ví dụ:
Input:
A = [1,2]
n = 4
Output: 5
Giải thích:
Tìm số cách để leo lên bậc thang thứ 4, mỗi lần có thể leo 1 hoặc 2 bước.
Số cách là: {1,1,1,1} {1,1,2} {1,2,1} {2,1,1} {2,2} = 5
Input:
A = [2,4,5]
n = 9
Output: 5
Giải thích:
Có 5 cách để leo lên bậc thang thứ 9 với khả năng leo 2 hoặc 4 hoặc 5 bậc thang mỗi lần.
Số cách là: {5,4} {4,5} {2,2,5} {2,5,2} {5,2,2} = 5
Số cách để leo tới bậc thang thứ n được cho bởi hệ thức truy hồi sau:
![]()
Gọi K là phần tử lớn nhất trong A.
Nó có thể được thực hiện trong thời gian O(m2K) bằng cách sử dụng phương pháp lập trình động như sau:
Hãy lẫy A = {2,4,5] làm ví dụ. Để tính F(1) = {f(1), f(2), f(3), f(4), f(5)}, chúng ta sẽ duy trì một mảng trống ban đầu và lặp lại nối Ai với nó và cho mỗi Ai chúng ta sẽ tìm số cách để đạt được [Ai-1, tới Ai].
Do đó, với A = {2, 4, 5]
Gọi T là mảng trống ban đầu:
Iteration 1: T = {2} n = {1,2} dp = {0,1} (Number of ways to reach n=1,2 with steps given by T)
Iteration 2: T = {2,4} n = {1,2,3,4} dp = {0,1,0,2} (Number of ways to reach n=1,2,3,4 with steps given by T)
Iteration 3: T = {2,4,5} n = {1,2,3,4,5} dp = {0,1,0,2,1} (Number of ways to reach n=1,2,3,4,5 with steps given by T)
Lưu ý: vì một số giá trị đã được tính toán (1,2 cho lần lặp 2...) chúng ta có thể tránh chúng trong vòng lặp.
Sau tất cả các lần lặp, mảng dp sẽ là: [0,1,0,2,1]
Do đó vectơ cơ sở F(1) cho A = [2,4,5] là:
0
1
0
2
1
Bây giờ chúng ta có vectơ cơ sở F(1), việc tính toán C (ma trận biến đổi) là khá dễ dàng.
Đó là một ma trận với các phần tử Ai, i+1 = 1 và hàng cuối cùng chứa các hằng số.
Bây giờ, các hằng số có thể được xác định bởi sự có mặt của phần tử đó trong A.
Vì vậy, đối với A = [2,4,5] các hằng số sẽ là c = [1,1,0,1,0] (Ci = 1 nếu K-i+1) có mặt trong A, hoặc 0 nếu 1 <= i <= K.
Do đó, ma trận biến đổi C cho A = [2,4,5] là:
0 1 0 0 0
0 0 1 0 0
0 0 0 1 0
0 0 0 0 1
1 1 0 1 0
Để tính F(n), công thức sau được sử dụng:
F(n) - Cn-1F(1)
Bây giờ chúng ta đã có C và F(1), chúng ta có thể sử dụng kỹ thuật Divide and Conquer để tìm Cn-1 và từ đó tìm ra kết quả đầu ra.
Dưới đây là code mẫu:
# Computes A*B when A,B are square matrices of equal
# dimensions)
def mul(A, B, MOD):
K = len(A);
C = [[0 for i in range(K)] for j in range(K)] ;
for i in range(1, K):
for j in range(1, K):
for k in range(1, K):
C[i][j] = (C[i][j] + A[i][k] * B[k][j]) % MOD;
return C;
def power(A, n):
if (n == 1):
return A;
if (n % 2 != 0):
# n is odd
# A^n = A * [ A^(n-1) ]
A = mul(A, power(A, n - 1), 1000000007);
else:
# n is even
# A^n = [ A^(n/2) ] * [ A^(n/2) ]
A = power(A, n // 2);
A = mul(A, A, 1000000007);
return A;
def initialize(A):
# Initializes the base vector F(1)
K = A[len(A)-1]; # Assuming A is sorted
F = [0 for i in range(K+1)];
dp = [0 for i in range(K+1)];
dp[0] = 0;
dp[A[1]] = 1; # There is one and only one way to reach
# first element
F[A[1]] = 1;
for i in range(2,len(A)):
# Loop through A[i-1] to A[i] and fill the dp array
for j in range(A[i - 1] + 1,A[i]+1):
# dp[j] = dp[j-A[0]] + .. + dp[j-A[i-1]]
for k in range(1,i):
dp[j] += dp[j - A[k]];
# There will be one more way to reach A[i]
dp[A[i]] += 1;
F[A[i]] = dp[A[i]];
return F;
def ways(A, n):
K = A[len(A) - 1]; # Assuming A is sorted
F = initialize(A); # O(m^2*K)
MOD = 1000000007;
# create K*K matrix
C = [[0 for i in range(K+1)] for j in range(K+1)];
'''
* A matrix with (i+1)th element as 1 and last row contains constants [ [0 1 0 0
* ... 0] [0 0 1 0 ... 0] [0 0 0 1 ... 0] [. . . . ... .] [. . . . ... .] [c(k)
* c(k-1) c(k-2) ... c1] ]
'''
for i in range(1,K):
C[i][i + 1] = 1;
# Last row is the constants c(k) c(k-1) ... c1
# f(n) = 1*f(n-1) + 1*f(n-2)
for i in range(1, len(A)):
C[K][K - A[i] + 1] = 1;
if (n <= K):
return F[n];
# F(n) = C^(n-1)*F
C = power(C, n - 1); # O(k^3Log(n))
result = 0;
# result will be the first row of C^(n-1)*F
for i in range(1, K+1):
result = (result + C[1][i] * F[i]) % MOD;
return result;
# Driver code
if __name__ == '__main__':
n = 9;
A = [ 0, 2, 4, 5] ;
# 0 is just because we are using 1 based indexing
print("Số lượng cách là = " ,ways(A, n));
# This code is contributed by gauravrajput1
Lưu ý: Cách tiếp cận này là lý tưởng khi n quá lớn, không thể dùng vòng lặp.
Ví dụ: Bạn nên xem xét cách tiếp cận này khi 1<= n <= 109 và 1 <= m,k <= 102.
Hy vọng rằng bài viết này sẽ có ích với các bạn.
Nguồn tin: Quantrimang.com
Ý kiến bạn đọc
Những tin mới hơn
Những tin cũ hơn
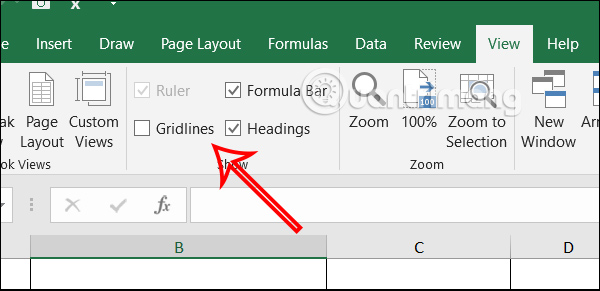 Hướng dẫn xóa dòng kẻ trong Excel
Hướng dẫn xóa dòng kẻ trong Excel
 Ước mơ mà không kèm hành động thì dù có cánh cũng không bao giờ bay tới đích
Ước mơ mà không kèm hành động thì dù có cánh cũng không bao giờ bay tới đích
 Làm được 3 điều này, cuộc sống mới thật sự nhẹ gánh, vô cùng đơn giản nhưng ít ai nhận ra để thay đổi
Làm được 3 điều này, cuộc sống mới thật sự nhẹ gánh, vô cùng đơn giản nhưng ít ai nhận ra để thay đổi
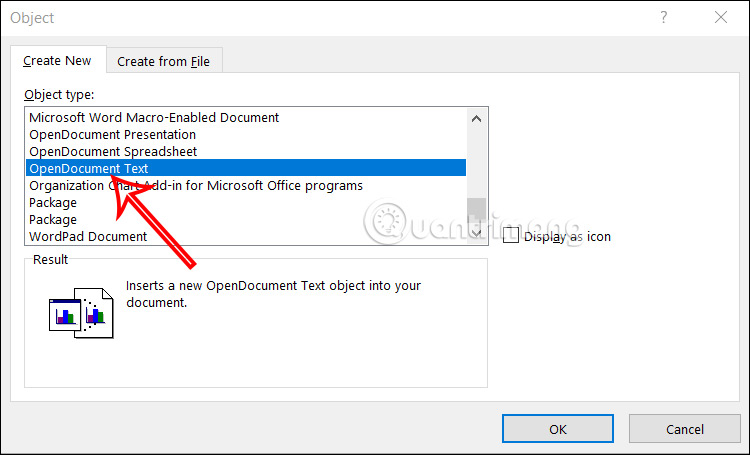 Hướng dẫn chèn code trong Word
Hướng dẫn chèn code trong Word
 20 tuổi và những thay đổi
20 tuổi và những thay đổi
 8 công cụ debugger Linux tốt nhất dành cho các kỹ sư phần mềm
8 công cụ debugger Linux tốt nhất dành cho các kỹ sư phần mềm
 Cách giả lập game PS2 trên máy Mac M1, M2 hoặc M3 với PCSX2
Cách giả lập game PS2 trên máy Mac M1, M2 hoặc M3 với PCSX2
 Cách chạy ứng dụng Windows trên Android bằng Winlator
Cách chạy ứng dụng Windows trên Android bằng Winlator
 Cách chuyển đổi tài liệu Word sang PDF
Cách chuyển đổi tài liệu Word sang PDF
 Cách xóa mật khẩu file PDF trên máy Mac
Cách xóa mật khẩu file PDF trên máy Mac
 Cách tạo trường tùy chỉnh WordPress để thêm siêu dữ liệu
Cách tạo trường tùy chỉnh WordPress để thêm siêu dữ liệu
 Lòng tự kiêu
Lòng tự kiêu
 24 ứng dụng chụp ảnh màn hình hữu ích dành cho macOS
24 ứng dụng chụp ảnh màn hình hữu ích dành cho macOS
 Cách chuyển thư mục Download sang ổ khác trên Windows 11
Cách chuyển thư mục Download sang ổ khác trên Windows 11
 Cách chụp màn hình máy Mac
Cách chụp màn hình máy Mac
 Cách gán các lõi CPU cụ thể cho một ứng dụng trong Windows
Cách gán các lõi CPU cụ thể cho một ứng dụng trong Windows
 Cách tạo hình ảnh bằng AI trong Krita
Cách tạo hình ảnh bằng AI trong Krita
 Niềm kiêu hãnh
Niềm kiêu hãnh
 Nợ chàng trai thanh xuân một lời cảm ơn và xin lỗi!
Nợ chàng trai thanh xuân một lời cảm ơn và xin lỗi!
 Xã giao
Xã giao
